2. What is the remainder when $1234\times5678 %speech$  is divided by 5?

3. A shape is made from five unit cubes, as shown.

What is the surface area of the shape?

4. The numbers p, q, r and s satisfy the equations p = 2,  p ×q = 20,  p × q × r = 202p × q × r × s = 2020 and $p\times q \times r \times s=2020 %speech% p times q times r  times s = 2020$.

What is the value of p + q + r + s ?

5. What is $\sqrt{123454321} %speech% square root of 123454321$ ?

6. There are fewer than 30 students in the A-level mathematics class. One half of them play the piano, one quarter play hockey and one seventh are in the school play.

How many of the students play hockey?

7. Official UK accident statistics showed that there were 225 accidents involving teapots in one year. However, in the following year there were 47 such accidents.

What was the approximate percentage reduction in recorded accidents involving teapots from the first year to the second?

8. What is the largest prime factor of $106^2-15^2 %speech% 106^2-15^2$ ?

9. In 2018, a racing driver was allowed to use the Drag Reduction System provided that the car was within 1 second of the car ahead. Suppose that two cars were 1 second apart, each travelling at 180 km/h (in the same direction!).

How many metres apart were they?

10. Six friends Pat, Qasim, Roman, Sam, Tara and Uma, stand in a line for a photograph. There are three people standing between Pat and Qasim, two between Qasim and Roman and one between Roman and Sam. Sam is not at either end of the line.

How many people are standing between Tara and Uma?

11. Two congruent pentagons are each formed by removing a right-angled isosceles triangle from a square of side-length 1. The two pentagons are then fitted together as shown.

‍
‍

‍
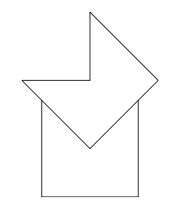
What is the length of the perimeter of the octagon formed?

12. A three-piece suit consists of a jacket, a pair of trousers and a waistcoat. Two jackets and three pairs of trousers cost £380. A pair of trousers costs the same as two waistcoats.

What is the cost of a three-piece suit?

13. The number $16! \div 2^k %speech% 16 factorial divided by 2 to the power of k$ is an odd integer. Note that $n!= 1\times2\times3\times\cdots \times (n-1)\times n %speech% n factorial = 1\times2\times3\times ellipsis \times (n-1)\times n$

What is the value of $k$?

14. Diane has five identical blue disks, two identical red disks and one yellow disk. She wants to place them on the grid below so that each cell contains exactly one disk. The two red disks are not to be placed in cells that share a common edge.

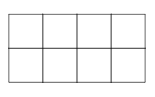
How many different-looking completed grids can she produce?

15. The shaded area shown in the diagram consists of the interior of a circle of radius 3 together with the area between the circle and two tangents to the circle. The angle between the tangents at the point where they meet is 60$^\circ %speech% degrees$.

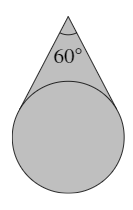
What is the shaded area?